Der Fehler in der Prozessanalytik
Die ideale Prozessregelung (Fig. 1) mit einem fehlerfreien Analysenmesssystem gibt es in der Praxis nicht (Fig. 2)
Der Messwert, der dem Verfahrentechniker eine Aussage über die zu erwartende Qualität seines Produktes ermöglicht, wird durch viele innere und äußere Störeinflüsse in seiner Prozessanlage beinflusst.
Gutes Regeln beginnt mit gutem Messen.
Der Hersteller eines Produktes muss einen Zielkonflikt lösen: Entweder ein Produkt herzustellen, dessen Zusammensetzung möglichst nahe den nicht genau bekannten wahren Werten kommt, oder dessen Eigenschaften sich im Verkaufserfolg bewährt haben, d.h. gut reproduzierbar sind. |
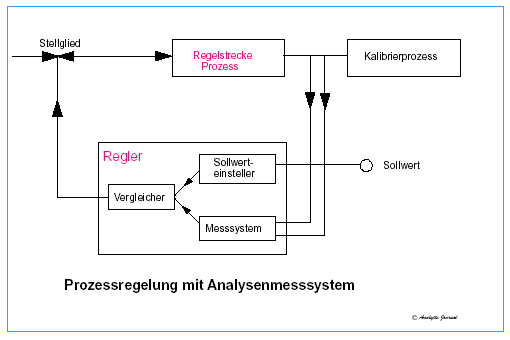
Fig. 1
|
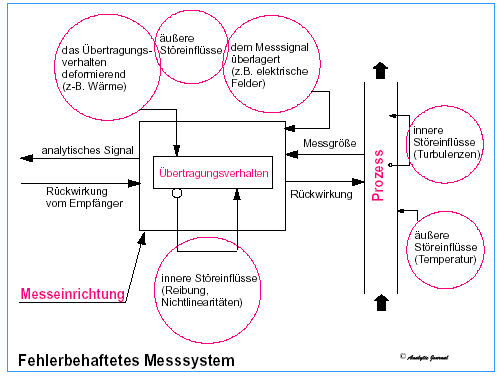Fig. 2
|
Andererseits zeigt die praktische Erfahrung im Umgang mit einem Produkt, dass oft gar nicht die genaue Kenntnis des wahren Messwertes notwendig ist, sondern die gute Reproduzierbarkeit der gewünschten Produkteigenschaften vollständig genügt.
Die Reproduzierbarkeit (Wiederholbarkeit) eines Ergebnisses kann zum Erfolg führen.
Für den Prozessanalytiker geht es also hier nicht um die Genauigkeit eines Messsystems, sondern darum, wie gut ein Messwert wiederholbar ist, eine präzise, wiederholbare, wenn auch ungenaue Messung ist ausreichend. Dazu genügt die Reduzierung der zufälligen Fehler (Fig. 3), systematische Fehler (Fig. 3) werden als (unbekannte) Größen im Wiederholungsprozess eingeschlossen.
Verusachen systematische Abweichungen merkliche Kosten, sollten mit einer Kalibrierung systematischen Fehler bestimmt werden (Fig. 4).
"Wahrer" Messwert
Für die Qualitätskontrolle (Zertifizierungen) oder für die Berücksichtigung der durch systematische Abweichungen verursachten Kosten genügt das Wiederholbarkeitskriterium nicht mehr, es müssen beide Fehlerarten, zufällig und systematische, ermittelt werden, das Ziel ist die möglichst genaue Ermittlung des analytischen Messwertes. Und dies heißt Kalibrieren.
Die Begriffe Reproduzierbarkeit und Genauigkeit und unterscheiden sich um ihre Bezugsgrößen:
Die Genauigkeit bezieht sich auf die Abweichung von einem "wahren" Wert, die Reproduzierbarkeit dagegen allein auf die Eigenschaften des Messsystems. |
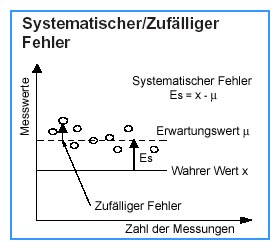
Fig. 3
|
Kalibrieren
Messgenauigkeit und Reproduzierbarkeit haben etwas gemeinsam: In jedem Falle muß hier kalibriert werden, da Messen immer Vergleichen mit einem bekannten Normal heißt!
Kalibrieren im Sinne einer Repro-duzierbarkeitsmessung hat nur das Ziel, systematische Fehler zu bestimmmen (Fig. 4).
Die ermittelte Kalibrierkurve hat aber nur dann Aussagekraft, wenn der zufällige Fehler des (mittleren) Meßwertes dagegen sehr klein ist.
Zufällige Fehler machen ein Analysenergebnis unsicher,
systematische Fehler machen es falsch.
Wird eine quantitative (Reproduzierbarkeit nicht ausreichend) Analyse im Prozess benötigt, muß der Zusammenhang zwischen Messgröße und wahrer Konzentration bekannt sein. Und dies ist schwierig zu realisieren: Denn die Kalibrierfunktion soll der realen Probe entsprechen und außerdem unter den gleichen Prozeßbedingungen ermittelt worden sein.
Daher gilt die Kalibrierfunktion nur für
- einen Dynamikbereich
- die vorliegende Stoffmatrix
- die festgelegten Arbeits- und Gerätebedingungen
Kalibrierfunktionen sind somit kaum übertragbar auf andere Systeme.
Man kann einen falschen Wert hervorragend genau messen!
Gutes Messen heißt gutes Kalibrieren!
Die Herausforderung an die Analytiker ist die zur Verfügungstellung verläßlicher und praktisch verwendbarer Normale, gleich ob sie bei Messungen der Reproduzierbarkeit oder in der quantitativen Analyse die Produktqualität letztendlich bestimmen.
Sind z.B. 100 ppm CO mit + 1% rel. Fehler zu bestimmen, so sollte der Fehler des Kalibrierwertes etwa + 0,1% rel. betragen, d.h. + 0,1 ppm CO!
Dies bedeutet aber auch, daß eine Kalibrierung mit nur einem Messpunkt (sehr oft angewendet!) ohne Kenntnis des zufälligen Fehlers bzw. des . Vertrauensbereiches sinnlos ist. |
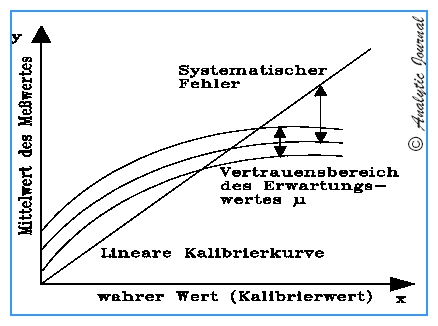
Fig. 4
|
Bezeichnung |
Definition |
Praxis |
Wahrer Wert
(ideal/true value) |
Der angezeigte Wert eines
idealisierten Messsysterms. |
Fig. 5 und Fig. 6
Der aus einer großen Zahl von Messungen bestimmte
Mittelwert.
Es werden auch international anerkannte
Kalibrierstandards
verwendet. |
Messwert
(value measured) |
Numerischer Wert einer physikalischen Größe,
die, unter den aktuellen Bedingungen,
aus den Informationen des Messinstruments
erhalten worden ist. |
Fig. 2
Messwerte als Ausgangssignale eines Analysensystems sind
behaftet mit den Fehlern
des Messgerätes und denen der Messung selber.
Der Grad ihrer Abweichung von dem Wahren Wert muss als
Messfehler
angegeben werden. |
| Erwartungswert |
Wird eine Messung unter bekannten und
gleichbleibenden Einsatzbedingungen
wiederholt, so schwanken die Messwerte
um den Erwartungswert, der als
Durchschnitt unendlich vieler
Messwerten resultieren
würde. |
Fig. 3
Art, Betrag und Häufigkeit der Abweichungen der Messwerte
von dem Erwarungswert, charakterisieren die
Reproduzierbarkeit eines Messwertes. |
Messfehler
- zufälliger - systematischer
(error, random error,
systematic error) |
Mess~Fehler ist der numerische Unterschied
zwischen dem Wahren Wert und dem Messwert.
Zufälliger Fehler
entstehen durch die
zufällige Kombination vieler Einzeleinflüsse,
sie sind nach Betrag und Vorzeichen zunächst
unbekannt (z.B. Ablesefehler).
Werden die Messungen unter bekannten und
gleichbleibenden Einsatzbedingungen
öfter wiederholt, so schwanken die Messwerte
um den Erwartungswert.
Systematischer Fehler
beschreiben die
permsnente Abweichung
des Wahren Messwertes von dem
Erwartungswert. Er ist
reproduzierbar
stets von derselben Größe und von
gleichem Vorzeichen. |
Fig. 3
Die Differenz zwischen dem Soll- und Istwert.
Zufälligen Fehler
werden mit statistischen
Methoden (Fehlertheorie) aus einer Messreihe
erfasst, die wiederum eine Aussage über die
Wahrscheinlichkeit ermöglichen, mit der die
Fehler unterhalb eines bestimmten Betrages bleiben.
Diese statistischen Methoden lassen also eine
Aussage zu über die Genauigkeit, mit der
der Erwartungswert mit einer bestimmten
Wahrscheinlichkeit ermittelt werden kann.
Genauigkeit ist nicht zu verwechseln mit Richtigkeit!
Systematische Fehler sollen durch vorbeugende
Maßnahmen im System vermieden sein oder,
da sie reproduzierbar sind, mit
Hilfe einer Kalibrierung
bestimmt werden.
Systematische Fehler bleiben im Verlaufe einer
Messung konstant bzgl. Größe und Vorzeichen
oder können sich ändern entsprechend einem
definiertem Gesetz,
wenn sich die Messbedingungen ändern einschließlich
des Übertragungsgesetzes der Messeinrichtung.
Zufällige Fehler machen ein Analysenergebnis unsicher
Systematische Fehler machen es falsch. |
Mess~Genauigkeit
System~Genauigkeit (accuracy) |
"Abwesenheit von Fehlern"
oder der
Grad der Übereinstimmung
eines angezeigten Wertes mit einem allgemein
anerkanntem Standard oder Wahren Wert.
Im Sinne dieser Definition müssten die Angaben in
technischen Daten über
"Genauigkeiten" als "Ungenauigkeiten"
bezeichnet werden, da diese sich ja auf den Fehler
eines Messsystem beziehen!
Z.B. ist mit der Angabe von + 1% für die
Mess~Genauigkeit eines
Analysensystems nicht gemeint, dass zu
99% Fehler auftreten!
Ausgesagt wird somit lediglich, dass das
System eine Mess~Ungenauigkeit
von + 1% hat
bzw. + 1% rel. Fehler zu einem Standard.
Mess~Genauigkeit ist nicht zu
verwechseln mit Richtigkeit!
Genauigkeit - und Präzision -
werden in der Praxis in der Laborsprach häufig
nebeneinander verwendet
ohne klaren statistischen Hiintergrund. |
Fig. 2
Die Messgenauigkeit
eines Analysensystems, das aus mehreren Teilen
besteht, ist solange unbekannt wie nicht kalibriert
wurde.
Wobei die Messgenauigkeit des Kalibriersystems
mindestens dreimal besser sein sollte
als die
des zu kalibrierenden.
Aus einer Reihe von Kalibrierzyklen
mit einem Analysengerät unter spezifischen
Bedingungen und definierter Prozedur werden die
maximale positive und negative Abweichung
von einem Standard bestimmt und in Prozent
der Messspanne ausgedrückt.
Die Angabe einer Messgenauigkeit ist damit
eine Aussage über die Qualität des Analysengerätes.
Fünf notwendige Angaben, um
Daten zur Mess~Genauigkeit vergleichbar
zu machen:
1. Zahlen mit aktuellem Messwert (nicht: Messbereich etc.)
2. Angabe des Messbereiches für den die Genauigkeit
garantiert wird.
3. Einschluss aller möglichen die Messungen
beeinflussenden Effekte wie Temperatur, Drift,
Hysterese etc.
4. Unabhängige Testlabors, da die Methodik den
Messfehler beinflusst.
5. Alle Angaben sollen sich auf den
2s-Vertrauensbereich (95%-Bereich) beziehen.
Angaben zur Mess~Genauigkeit
sollten daher mindestens so aussehen:
"X% der aktuellen Ablesung über einen
Messbereich von Y". |
| Messunsicherheit |
Ist die Angabe des
Fehlers, der mit einer bestimmten
Wahrscheinlichkeit nicht überschritten
wird (Vertauensbereich der Messung).
Dies im Unterschied
zu der Angabe von Fehlergrenzen,
die als äußerste Abweichung vom
Erwartungswert
für das
Messsystem garantiert werden. |
Fig. 7
Es können auch Fehler auftreten, die gößer sind
als angegeben.
Um diese mit zuerfassen, müsste die
Messunsicherheit mit einer Wahrscheinlichkeit
von z.B. 99% angegben werden. |
Fehlergrenzen
(accuracy rating) |
Fehlergrenzen sind die für ein Messsystem
garantierten äußersten Abweichungen
vom Erwartungswert bei definierten
Betriebsbedingungen.
Dies
im Unterschied
zu der Angabe der Messunsicherheit,
für die jede Fehlerangabe bedeutet, dass
dieser Wert nur mit einer gewissen
Wahrscheinlichkeit nicht überschritten
wird.
|
Fehlergrenzen werden meistens
absolut oder in Prozent der Messspanne
oder des jeweiligen
oberen Messbereichsendes
angegeben.
Beispiel: . +1°C oder +0,5% der Messsapanne
von 15 ... 50 ppm
oder
+0,5% des oberen Messbereichendes von 50 ppm.
Die Angabe von Fehlergrenzen für ein Messsystems
bedeutet, dass alle Fehlerquellen (systematische
und zufällige Messfehler, Hysterese, Totbereich etc.)
damit erfasst worden sind.
Die Angabe der Fehlergrenzen für ein Messystem ist
eine
entscheidende Aussage über seine Qualität im
Prozessbetrieb.
Da diese Werte aber immer an bestimmte Betriebs-
und Einsatzbedingungen geknüpft sind,
sollte sich der Analytiker die
Fehlergrenzen für seinen speziellen Einsatz
garantieren lassen. |
Wiederholbarkeit
(repeatability) |
Wiederholbarkeit ist
der Grad der Übereinstimmung
zwischen den Ergebnissen einer Anzahl
direkt aufeinander folgender Messungen
für den denselben Eingangswert und unter
denselben Betriebsbedingungen,
immer in
gleicher Richtung
und für den vollen
Arbeitsbereich (0 ... 100% für
das Eingangs- und das Ausgangssignal))
gemessen.
Bemerkung: Eigentlich wird immer die
NIcht-Wiederholbarkeit gemessen
und
als Wiederholbarkeit in Prozent von der
Messspanne angegeben.
|
Wiederholbarkeit ist die
maximale Abweichung der Messwerte
aus mehreren Kalibrierzyklen
unter gleichen Betriebsbedingungen.
Sie wird angegeben
in Prozent der Messspanne
Beispiel: 0.05% der Messsapanne 10 ... 25 ppmr
Der Hysterese-Fehler ist nicht eingeschlossen. |
Reproduzierbarkeit
(reproducibility) |
Reproduzierbarkeit ist der
Grad der Übereinstimmung
innerhalb eines
bestimmten Zeitraumes
zwischen den Ergebnissen aus einer Anzahl von
Messungen, für
denselben
Eingangswert und unter denselben
Betriebsbedingungen,
in beiden Richtungen gemessen.Bemerkung
Eigentlich wird immer die
NIcht-Reproduzierbarkeit
innerhalb
eines bestimmten
Zeitraumes gemessen
und als
Reproduzierbarkeit
in Prozent
von der
Messspanne angegeben.
|
Reproduzierbarkeit ist die
maximale Differenz
zwischen den registrierten Ausgangssignalen
für einen gegebenen Eingangswert
innerhalb eines Zeitintervalls.
Diese Differenz wird in Prozent der
Messspanne pro Zeitntervall angegeben.
Beispiel: 0.2% der Messspanne
10 ... 20 ppm während eines Drei-Tage-Tests.
Bemerkungen
1. Reproduzierbarkeitsmessungen schließen ein:
Hysterese, Drift, Unempfindlichkeitsbereich
und die Wiederholbarkeit.
2. Zwischen den verschiedenen Messungen kann das
Eingangssignal über den Messbereich variieren
und innerhalb des normalen Bereiches
können auch die Betriebsbedingungen geändert sein. |
Drift
(drift - point drift) |
Drift ist die
ungewollteÄnderung
des Verhältnisses des Ausgangs-
zum Eingangssignal.
|
Drift ist die
maximale Änderung
eine einzelnen Ausgangssignals
während einer bestimmten Zeit
bei konstantem Eingangswert und gleichbleibenden
Betriebsbedingungen.
Angabe in
Prozent der Spanne
des Ausgangssignals für einen bestimmten Messpunkt.
Beispiel: die "Drift in der mittleren Messspanne
beträgt 0,1% der Spanne des Ausgangssignals über
24 Srunden".
Wichtig: Nullpunktsdrift |
Kalibrieren
(calibrate) |
Ermittlung des Mess~Fehlers
durch den Vergleich der Messergebnisse eines
Messsystems
mit einem anerkanntem Standard
Kalibrieren hat nichts mit Eichen zutun!! Eichen
ist im Wesentlichen
ein administrativer
Akt einer Behörde. |
Fig. 4
Für eine Kalibrierung soll
- die Zahl der Messpunkte größer als fünf sein
und
- den ganzen Messbereich abdecken.
- Betriebsbedingungen sollen konstant gehalten werden,
- Einlaufverhalten und Warm-up-Phasen sind zu beachten.
- Das Messgerät soll unter den jeweiligen
Einsatzbedingungen und am Einsatzort mit allen
peripheren Systemen kalibriert werden.
- Das Kalibriergas soll der Zusammensetzung
des Prozessgases entsprechen.
Die "Kalibrierkurve" wird als
Abweichungskurve
dargestellt, d.h. die Differenz zwischen Messwert und
dem entsprechenden Wahren Wert wird
geplottet, für beide Richtungen (steigende bzw.
fallende Messwerte). |
Linearität
Toleranzband |
Zwei Defintionen
für den Begriff Linearität sind gebräuchlich:
1. Referenzgerade durch den Nullpunkt
und den Endpunkt
des Vollauschlags.
Die
LInearität wird dann als
maximale Abweichung im Sinne
einer Fehlergrenze
angegeben.
2. Die Referenzgerade wird so durch
die Messpunkte der
Kalibrierung gelegt,
dass die Summe
der Fehlerquadrate
minimal wird ("lineare Regression").
Die Linearität wird dann als
maximale Abweichung im Sinne
der Messunsicherheit
angegeben.
|
In der Prxis wird häufig der Begriff
Toleranzband
verwendet, der sich auf jeweils eine der nebenstehenden
Definitionen bezieht.
Ist der Zusammenhang zwischen Messgröße und
Messwertanzeige linear, so gibt die Angabe der
Linearität die Abweichung von dieser Geraden an.
Meist wird die
maximale Abweichung von der Geraden in Prozent
des Anzeigebereiches angegeben.
|
Hysterese
Umkehrspanne
(hysteresis) |
Hysterese ist die
Differenz der Anzeigen,
die man für den gleichen Wert der
Messgröße erhält,
wenn einmal
von kleineren zu größeren
und zum Anderen
von größeren zu kleineren Messwerten
gegangen wird. |
Die Ursachen sind ganz unterschiedlicher Natur:
- mechanisches Spiel (Lose)
- trockene Reibung
- elastische Nachwirkung
- Hysterese magnetischer Materialien
Die Bezeichnug Hysterese hat sich in der Messtechnik
als Sammelbegriff für alle Phänomene dieser Art eingebürgert.
Sie wird angegeben in Prozent der Messspanne. |
Auflösungsvermögen
(resolution) |
In der Optik
definiert als der
Winkelabstand
nahe beieinander liegender Details
eines Objektes, für den
eine deutlich
unterscheidbare Abbildung
dieser Details noch möglich ist.
In der Messtechnik:
die Registrierung
zeitlich dicht
aufeinander folgender Signale. |
In der Prozessanalytik
hat das Auflösungsvermögen bei den optischen
Spektrometern eine Bedeutung als"eingebaute"
physikalische Größe,
ist aber für den Anlagenbetrieb, der stets weit entfernt von
Messgrenzen erfolgt, von
geringerer Bedeutung.
Bei digitalen Anzeigen wird häufig auch eine "Auflösung"
angegeben. Diese hat mit den
analytisch-physikalischen Eigenschaften des Messsystems
aber nichts zutun.
Diese "Auflösung" beschreibt nur die Art der elektronischen
Widergabe
eines Messwertes und sollte nur soviel Digits haben, wie
der Fehler des Analysensystems den Messwert beeinflusst.
Displays, auch mit vielen Digits, erlauben
keine Aussagen über die Messgenauigkeit. |
Bürde
(Max. load) |
Bürde ist die
Rückwirkung des Messvorganges
auf die Messgröße.
Der zur Erfassung des Messwetes dienende
Fühler (Sonde) beeinflusst
in mehr oder weniger starken Weise den Prozess
bzw. die zu messende Größe. |
Bei der Messung einer
nichtidealen Spannungsquelle
mit einem Drehspulinstrument bewirkt der zur
Messanzeige
benötigte elektrische Strom am
inneren Widerstand der Spannungsquelle
einen
Spannungsabfall.
Die dadurch entstehende
Fehlanzeige
bei gegebener Belastung durch das Messgerät ist somit von der
Größe des äußeren Widerstandes, der Bürde,
abhängig.
Der in den technischen Daten
angegebene Wert für die
maximale Bürde
eines Analyseninstrumentes ist der maximale äußere
Widerstand, bis zu dem der
Messfahler des Gerätes innerhalb der angegebenen
Grenzen liegt. |
Präzision
(precesion) |
Anteil der zufälligen Fehler im Messergebnis |
Präzision -
und Genauigkeit - werden in der Praxis
in der Laborsprach häufig nebeneinander verwendet
ohne klaren statistischen Hiintergrund. |
Empfindlichkeit -
(sensitivity) |
Steigung der Eichkurve (Eichgeraden) |
In der Praxis
gehört zu jeder Zahlenangabe zur Empfindlichkeit die
Angabe des entsprechenden Messbereiches.
Im Spurenbereich sind derartige Angaben
nicht sinnvoll.
Hohe Empfindlichkeiten sind im
Prozessbetrieb nicht immer anzustreben,
wenn der Prozess nicht die entsprechende
Reaktion zeigen kann. |
Kritischer Wert -
Nachweisschwelle |
Der kritische Wert entscheidet, ob ein
Messwert reel ist oder nicht.
Statistische Definition (s. Fig. 8): Lc = ka sB
mit sB als Standardabweichuing des
Blindwertes und
ka als statistischer
Sicherheit |
Fig. 8 und Fig. 9
Der kritische Wert (s. Fig. 8) entscheidet, ob ein
Messwert zur Nachweisgrenze oder zum Blindwert
gehört.
Die Wahrscheinlichkeit hierfür wird als gleich groß angenommen. |
Nachweisgrenze -
qualitative Analyse
(detection limit) |
Dieser Begriff bezieht sich
nur auf die qualitative Analyse.
Sie ist die
kleinste Menge/Konzentration
eines Elementes, die man mit einer
geforderten
statistischen Sicherheit
qualitativ
nachweisen kann.
Bemerkung:
Von den Grundlagen der analytischen
Chemie her
muss zwischen dem
qualttativen Nachweis und der
quantitativen
Bestimmung
unterschieden werden werden.
In der Praxis wird leider der
Begriff Nachweisgrenze
sowohl für qualitative als auch für
quantitatve Analysenmethoden verwendet. |
Fig. 8 und Fig. 9
Die
Messunsicherheiten in der Nähe der
Nachweisgrenze sind sehr groß,
da diese der kleinste gefundene Gehalt ist, der sich vom
Gehalt Null gerade noch unterscheidet.
Eine Fehlerangabe zu einer Nachweisgrenze ist daher sinnlos.
Zahlenangaben zu diesen Grenzen sind an das
jeweilige Analysenverfahren gebunden
und sollen mit angegeben werden.
Nachweis- und Bestimmungsgrenze
kennzeichnen die reale Leistungsfähikeit
des Analysenverfahrens, wobei der
technische Aufwand noch zu beachten ist. |
Bestimmungsgrenze
quantitative Analyse
(measuring limit) |
Dieser Begriff (s. Fig. 8) bezieht sich nur auf die
quantitative Analyse.
Sie ist die
kleinste
Menge/Konzentration
eines Elementes, die man mit einer
geforderten
statistischen Sicherheit
quantitativ
nachweisen kann.
Bemerkung:
Von den Grundlagen der analytischen Chemie
her muss zwischen dem
qualttativen Nachweis und
der quantitativen Bestimmung
unterschieden werden.
In der Praxis wird leider der Begriff Nachweisgrenze
sowohl für qualitative als auch für quantitatve
Analysenmethoden verwendet.
|
Fig. 8 und Fig. 9
Sie wird mit der
maximal zulässigen (relativen)
Standardabweichung
festgelegt.
Zahlenangaben zu diesen Grenzen sind an das jeweilige
Analysenverfahren gebunden
Nachweis- und Bestimmungsgrenze
kennzeichnen die reale Leistungsfähikeit
des Analysenverfahrens, wobei der technische
Aufwand noch zu beachten ist. |
Blindwerte
(blank value) |
"Analytischer Störpegel".
Ursachen sind
- Unzulänglichkeiten der
Messinstrumente,
- elektronisches Rauschen,
- Mess- und Ablesefehler,
- Querempfindlichkeiten
zu anderen Elementen,
- unsaubere Proben.
|
Fig. 8 und Fig. 9
Die zahlenmäßige Erfassung des Blindwertes
ist unbedingt erforderlich, denn erst dann kann
man sich sicher der Nachweisgrenze nähern.
Zur Bestimmung werden zwei Verfahren verwendet:
1. Mindestens 20 Einzelanalysen ohne
Anwesenheit des zu messenden Elementes.
2. Aus dem Schnittpunkt der Kalibriegeraden
mit der Abzisse (Fig.7)
Blindwerte sind je nach Labor verschieden. |
| Standardabweichung |
Fig. 7 |
Zur Standardabweichung gehört immer die
Angabe des Vertauensbereiches. |
Vertrauens~,
Toleranzbereich |
Die Breite der Gauß-Kurve und die entsprechende
Fläche unter der Gaußkurve |
Fig. 5
Industrie: 2s-Regel (95%), Biologie:3s-Regel (99,73%) |
